基于I-PSO算法的沙棘果振动分离机械手轨迹分析与优化
本文利用I-PSO算法研究了空间机械臂沙棘果振动分离轨迹的最优时间规划。第一步是分析机械臂关节的运动,其运动范围和速度受到限制,结合3-5-3多项式插值,提出了一种具有自适应惯性权重和异步学习因子的改进粒子群优化算法,并给出了具体流程。实验图像和数据表明,改进的粒子群优化算法能够保证关节加速度和速度的连续性,最优振动轨迹时间为0.536539094 s,与规划系统轨迹时间0.71022 s相比,速度提高了24.5%。正交实验结果表明,平均落果率达到96.19%,验证了I-PSO算法对沙棘果实分离振动轨迹最优时间规划的有效性和可靠性。
介绍
沙棘(Hippophae rhamnoides L.),又名醋柳、黑刺李;胡颓子科沙棘,被希腊称为“闪亮的马” 1,2,3。沙棘根部因根瘤菌固氮作用而具有抗寒、抗旱、耐瘠薄的能力,是改良土壤、改善生态环境的优质生态树种4 , 5 , 6。由于其附着力强,成熟的果实在很小的外力作用下就会被压碎,导致采收非常困难。机械采收已成为制约沙棘产业规模化工业化生产的瓶颈问题7。其中,机械手的振动轨迹分析和优化方法对于实现沙棘果实振动分离机械化至关重要。
机械臂时间轨迹规划是在给定任务和约束条件下确定机械臂轨迹的过程。对于保证安全、提高效率、提高精度、适应动态环境、实现协调运动等具有重要意义。机械臂的时间轨迹规划关系到企业时间效率的限制,也是机器人运动学的重要研究点8 , 9 , 10 , 11。赫克托等人。通过有限元分析模拟和预测了水果的振动行为,为进一步改进水果分选设备和技术提供了理论依据12。托雷格罗萨等人。利用人工视觉技术,在施加振动的情况下,用摄像头记录水果在振动过程中的运动,并通过图像处理和分析技术提取柑橘类水果的分离效果13。为了优化机械手的轨迹,Yong 等人。提出了一种基于过渡矩形的遗传算法优化方法14.李彦等人。将生物学的协调运动特性应用到二维空间机械臂的运动规划中,提出了一种新的生物学方法来规划人工机械臂的运动15。浩田等人。提出了一种基于神经网络的机器人机械臂轨迹规划方法,并通过多次实验验证了该方法的可行性和有效性16。上述研究为机械臂轨迹规划与优化研究做出了巨大贡献。同时我们也可以看到,多目标优化方法并不完善,传统的粒子群优化算法很容易陷入局部寻优,导致收敛速度慢、局部优化不平衡等问题。因此,为了解决传统算法容易陷入局部最优的问题,本研究选择对沙棘的分枝采摘和振动分离轨迹进行分析,并通过改进的PSO算法对轨迹时间进行优化。为研究沙棘果振动分离轨迹提供实验依据,提高沙棘果振动分离机械手的工作效率和可靠性,改善生产环境,推动机器人技术的发展和进步。
材料和方法
材料
沙棘来自新疆生产建设兵团第九师170团沙棘种植基地。该品种为“深秋红”品种,树龄4年左右。株距2~4m左右,株高2~2.5m左右,宽度2m左右。
方法
轨迹分析
选择轨迹规划方法
轨迹规划分为关节空间轨迹和任务空间轨迹。角度-空间轨迹:首先是两个时间点的夹角进行插补以保证角度的连续性,然后进行角度插补的逆运动学轨迹规划。任务空间轨迹:首先,对位置位移进行插值保证位移的一致性,然后规划该位置在空间中的逆运动学轨迹。
由于机械臂可以在未知的关节角度下确定任务空间的位置,因此本研究选择任务空间方法进行轨迹规划。
拾取轨迹规划
JTRAJ 功能可快速、平稳地生成机器人轨迹。通过关节空间轨迹(JTRAJ)函数生成的连续多项式轨迹可以实现采摘过程中树枝和树叶的掉落。通过输入起始位置、终止位置和时间步长得到该时间点的关节位置,并得到规划轨迹17。该轨迹保证了关节加速度和速度的连续性,更符合机器人的实际运动。
从图1可以看出 。可见JTRAJ函数在规划拾取轨迹时是平滑的,轨迹有轻微的振动,有利于拾取过程中枝叶的掉落。

JTRAJ函数用于获取机械臂的参数。
振动轨迹规划
沙棘果振动分离的路径规划是通过合理的设计和控制,使系统按照预定的路径或路径振动。

微信公众号:计算机程序吧
沙棘果振动分离机械臂的关节空间和任务空间轨迹规划点分别设置为(0,0,0.2),(−0.1,0.2,0.4),(−0.2,0,0.1),(−0.1,− 0.2, 0.4), (− 0.1, − 0.2, 0.4), (− 0.1, − 0.2, 0.4), (− 0.1, − 0.2, 0.4),最后一个循环返回初始位置(0,0,0.2) 。仿真结果如图2所示 。
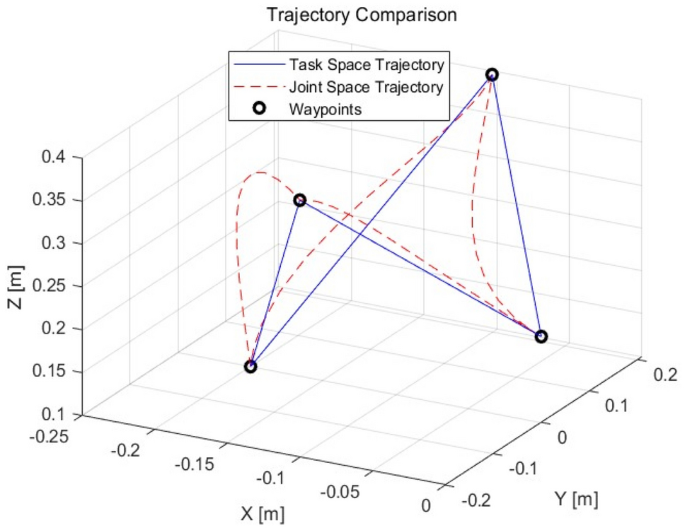
关节角度和任务空间角度的轨迹。
如图 3所示,关节任务所需的空间轨迹时间为0.71022 s,关节角度轨迹规划时间为0.13634 s。从图 4可以看出,任务空间整体轨迹规划平滑,角度空间轨迹规划直接,轨迹变化较大,对机械臂有一定影响。
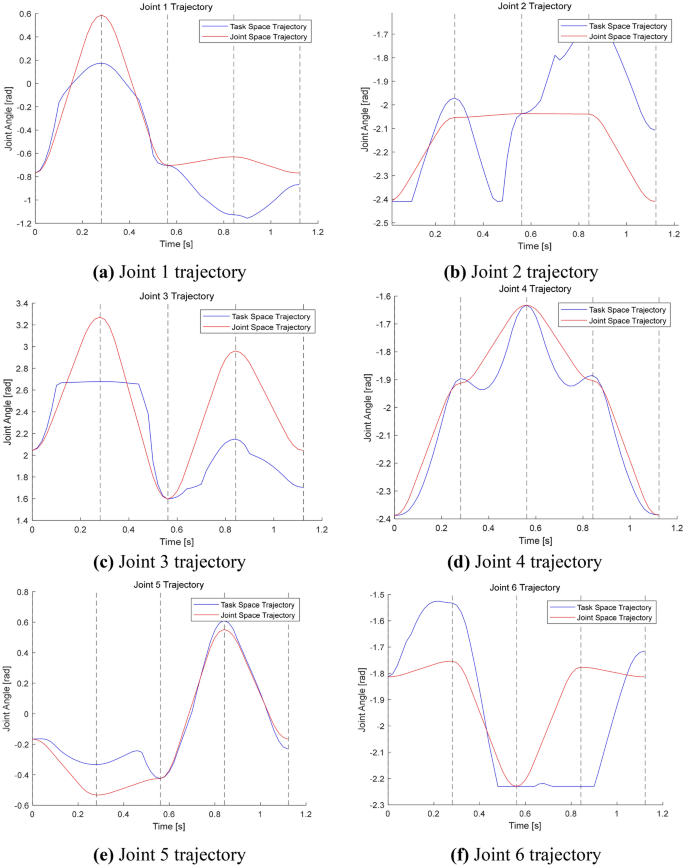
机械臂各关节的振动轨迹。
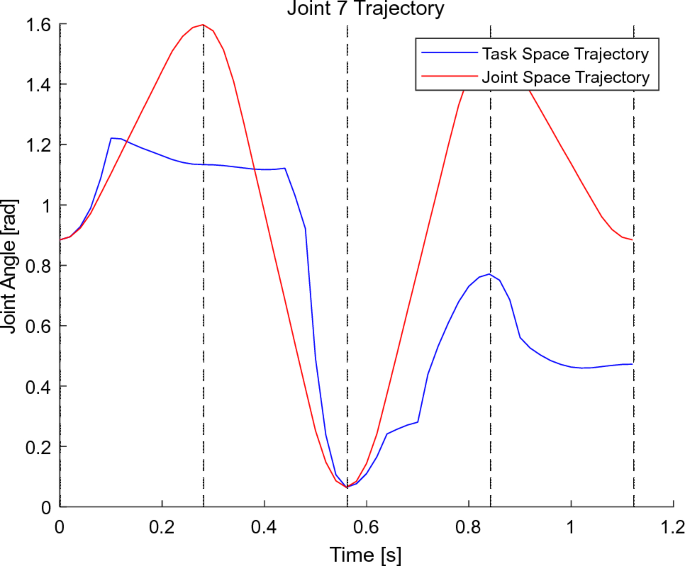
机械手的末端夹紧元件的轨道。
基于I-PSO算法的振动轨迹时间优化
粒子群优化
粒子群优化(PSO)是一种群体智能全局随机搜索算法,模拟群体的迁徙、觅食行为,融合个体认知、社会影响等社会心理学概念 18 ,进化算法-EA的成员,简称PSO 19。
粒子群速度更新公式:
:颗粒数;:颗粒尺寸数;:迭代次数;:惯性重量;:个人学习因素;:小组学习因素;:区间[0, 1]内的随机数;: 这粒子的维速度向量在里面第-次迭代;: 这粒子的维位置向量在里面第-次迭代;:粒子的历史最优位置在- 维度在第-次迭代;:历史最优位置- 维度在第-次迭代。
(惯性部分):由惯性权重和粒子速度决定,表明粒子之前对其运动的信任状态。(个体认知):粒子的自我认知,即粒子自身经验的一部分,可以理解为粒子当前位置与个体历史中最优位置的距离和方向。(社会共享):粒子群之间的信息共享和协作,即来自群体中其他粒子的优化经验,可以理解为粒子当前位置与群体历史最优位置之间的距离和方向。
改进的粒子群优化算法(I-PSO)
惯性权重w和学习因子,,而传统粒子群优化算法的其他参数是固定的。在优化过程中,算法容易陷入局部最优陷阱等问题,导致收敛速度慢、局部优化不平衡、全局优化误差20。使用PSO算法规划机械臂的最优时间时,需要保证机械臂关节速度边界的约束和加速度的连续性。因此,本文通过引入自适应惯性权重、异步学习因子和3-5-3多项式插值粒子群优化来优化机械臂的运动时间。改进的粒子群优化算法简称I-PSO。
自适应惯性权重:
:分别为迭代次数的当前值和最大值;:惯性权重的最大值和最小值。
在粒子群优化中,惯性权重W可以通过控制搜索区域21的大小来平衡全局和局部优化能力以及收敛速度。当使用较大的惯性权重W时,粒子运动的惯性和搜索扩展空间的能力增强,有利于全局优化,跳出局部极值,不陷入局部最优,局部优化能力将得到增强,从而使算法能够快速收敛到最优解22。传统的PSO算法仅增加或减少惯性权重,无法应对复杂的现实环境中不断变化的需求。因此,本文引入了一种自适应惯性权重,可以根据复杂的搜索情况在不同阶段实现不同的权重,如公式(2)所示。在PI-PSO算法前期,由于问题空间较大,为保证搜索速度和精度的平衡,PI-PSO算法前期采用较大的惯性权重,以达到较高的全局搜索能力以获得正确的解决方案。后期通过使用较小的惯性权重来提高局部搜索能力,以提高收敛精度。
异步学习因素,:
:个体认知加速系数;:社会共享加速系数。
由式(1)可知,学习因子影响粒子的“个体认知”能力,应该随着搜索迭代次数的增加而逐渐减小,而学习因子影响粒子的“社交共享”能力,它应该随着搜索迭代次数的增加而增加。由于学习因素和传统粒子群优化的参数都是固定的,这会影响算法的优化速度和求解精度的平衡。因此,本文引入异步学习因素,如式( 3 )和( 4 )所示。在优化初期,改进算法保证初始个体认知解的区域大于群体认知解的区域,并且保证粒子不陷入局部极值陷阱,使得群体具有较强的全局性。优化能力和收敛速度。
3–5–3 多项式插值:
: 的轨迹函数的时间段联合的;代表- 段系数- 分段插值函数-节段铰接轨迹。系数的矩阵形式如式( 9 )所示,式( 8 )为系数解。
b:包含未知数的系数;A:简单的时间函数;H:机械臂相对于时间T的运动矩阵。
(I-PSO)算法目标内容描述(流程图)
改进的I-PSO算法流程图如图 5所示。I-PSO 算法基于传统的粒子群优化(PSO-RRB 算法)。通过改进自适应惯性权重和异步学习因子,可以保证优化速度和精度之间的多项式插值。
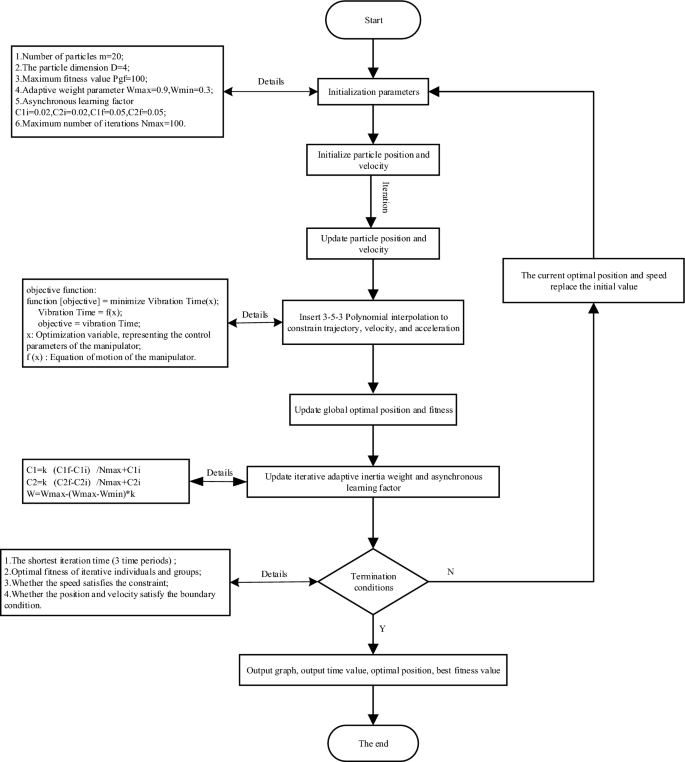
I-PSO 算法流程图。
方法论声明
本研究表明,机械臂振动轨迹的实验和模拟,包括沙棘材料的采集,均符合相关机构、国家和国际标准。
结果
根据补充材料的实验数据,仿真实验中在最优时刻附近各轴的优化结果如下:通过多组仿真实验得到的机械臂在X轴上的轨迹规划与实验最接近平均值如图 6所示。通过多次仿真实验,机械臂在Y轴上的轨迹规划最接近实验平均值,如图 7所示。通过多次仿真实验,机械臂在Z轴上的轨迹规划最接近实验平均值,如图 8所示。
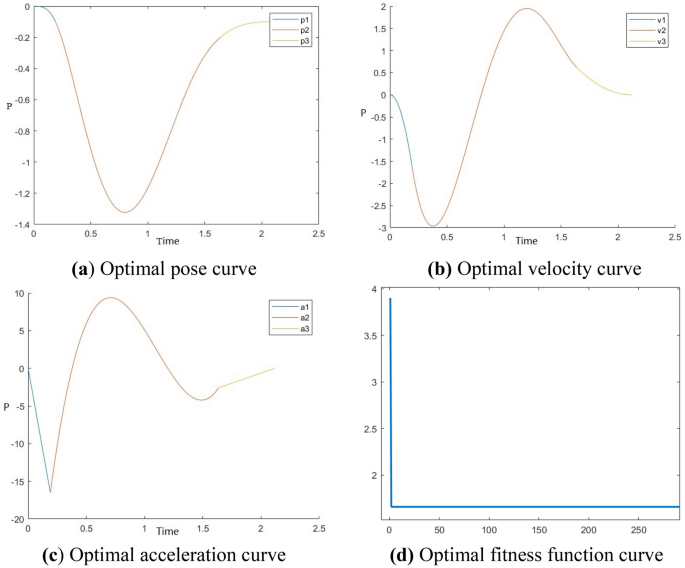
X轴机械臂最优时间轨迹规划。

机械臂Y轴最优时间轨迹规划。
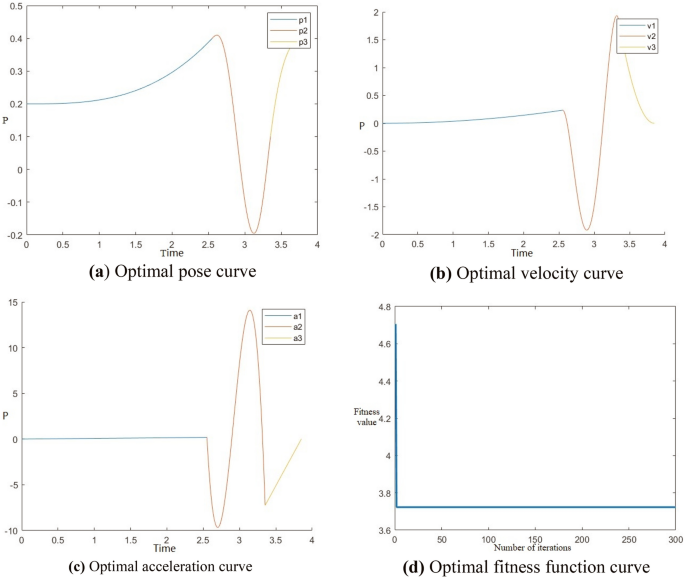
机械臂Z轴最优时间轨迹规划。
当通过算法优化机械臂振动轨迹的时间时,X轴和Z轴的位姿波动较大。进行了四组仿真实验以进行最优时间轨迹规划。结果表明,其中一组实验数据不合格,其余六组最佳时间分别为0.396 s、0.483 s、0.735 s和0.700 s、0.408 s、0.498 s。对Y轴轨迹进行三组仿真实验,最佳时间分别为0.802 s、0.539 s、0.533 s。X轴平均最佳时间为0.538 s;Y轴平均最佳时间为0.536 s;Z轴平均最佳时间为0.535秒。
为了验证算法的有效性和可靠性,采用方差分析的方法对沙棘枝条的振动轨迹进行了分析。得到沙棘的果实数据如表1所示。
采用SPSS软件对落果率方差进行分析,体间效应检验表如表2所示。
表2中,修正模型的显着性大于0.05,因此修正模型与方差模型整体分析没有显着性差异,且效果为振动频率>振动幅度>振动时间。
结论
基于3-5-3多项式插值函数,利用改进的粒子群优化系统(I-PSO)对沙棘的振动轨迹进行及时优化,仿真实验结果如下:
- (1)
本研究中任务空间的轨迹规划可以实现拾取过程中树枝和树叶的掉落,并能保证轨迹关节位姿、速度和加速度的连续性,更加接近机器人的实际运动。
- (2)
本研究采用改进的粒子群优化算法(PSO-RRB算法结合3-5-3多项式插值)来选择机械臂在最短时间内完成运动并满足速度约束的最佳时间,仿真结果表明:结果表明,平均最优联动时间为0.536539094 s,比JTRAJ函数规划的原轨迹时间0.71022 s提高了24.5%,证明了I-PSO算法对于时间轨迹优化的有效性和优越性,为开发做出贡献对相关机械臂的轨迹规划及优化进行研究,可减少机械臂的运动时间,提高沙棘果实采收的工作效率,对传统算法的优化,便于促进人工智能的发展轨迹也保证了机器人终端姿态的连续性。
- (3)
利用SPSS对沙棘枝条振动正交试验进行方差分析。数据表明,优化算法平均落果率可达96.19%,比原JTRAJ函数轨迹规划的平均落果率95.32%提高了0.87%,验证了I-PSO算法寻优的有效性和可靠性。对沙棘果实分离振动轨迹的时间规划进行了验证。但从实验数据中我们可以看出,加速度变化越快就会产生影响,后期需要从这方面进行研究。
参考
-
庞迪尔,S.等人。沙棘的民族药用、植物化学和皮肤病学作用:综述。J. Ethnopharmacol。 266、113434(2021)。
-
Surmiński, J. 沙棘 ( Hippophae rhamnoides L.) 的发生和特性。西尔万 152 (4), 68–74 (2008)。
-
刘,X.等人。沙棘混浊汁稳定性研究 中国酿造 37 (6), 136–139 (2018)。
-
刘国国,沙棘拉丁名的由来.中国保健食品, 10 , 80 (2018).
-
Gâtlan, AM 和 Gutt, G. 植物性饮食中的沙棘。沙棘果实成分的分析方法:营养价值、应用和健康益处。国际。J.环境。资源。公共卫生 18 (17), 8986 (2021)。
-
Bonciu,E.等人。沙棘水性水果提取物对可持续农业生态系统的生物刺激潜力的细胞遗传学研究。工厂 9 (7), 843 (2020)。
-
严,D.等人。机械化葡萄采摘对果茎系统影响的振动分析及试验研究 百奥系统。工程师。 227 , 82–94 (2023)。
-
童,HY等人。管棒拆捆机器人系统及轨迹规划研究 组合。马赫。工具自动化 马赫。技术。 7、40-43(2022)。
-
陈,H.等人。船舶横摇运动的海上起重机时间最优轨迹规划方法 J.富兰克林研究所。 359 (12), 6099–6122 (2022)。
-
阿布-达卡,FJ等人。工业机器人最短时间轨迹规划问题的进化算法的统计评估。国际。J.Adv。制造商。技术。 89、389-406(2017)。
-
Okuyama,IF,Maximo,MROA 和 Afonso,RJM 考虑防滑约束的差动驱动移动机器人的最短时间轨迹规划。J. 控制自动化。电。系统。 32 (1), 120–131 (2021)。
-
Tinoco, HA & Peña, FM小粒咖啡的有限元分析。哥伦比亚利用强制振动实现选择性分离。振动 1 (1), 207–219 (2018)。
-
托雷格罗萨,A.等人。利用人工视觉分析柑橘类水果振动脱离情况。百奥系统。工程师。 119,1-12(2014)。
-
Yong,G.等人。机械臂轨迹规划中基于跳跃矩形的遗传算法优化 J. Phys。会议。序列。 1389 (3), 032041 (2019)。
-
李,Y.等人。机器人操纵器运动规划的仿生方法。神经计算 312 , 147–155 (2018)。
-
田,H.等人。基于神经网络的机械臂路径规划。英特尔。控制自动化 10 (8), 39–47 (2019)。
-
王红,赖阳,陈文。托卡马克检测机械臂操作任务限制下的时间最优轨迹规划。融合工程。设计 113 , 57–65 (2016)。
-
袁金涛,刘建,邹思乐,基于粒子群优化的工业机器人多目标最优轨迹规划。工业仪器。自动。 5、73-79(2021)。
-
Kennedy, J. & Eberhart, R. Particle swarm optimization. in Proceedings of ICNN'95-International Conference on Neural Networks. IEEE, 4, 1942–1948 (1995).
-
Fan, SKS, Liang, Y. & Zahara, E. 用于多模态函数全局优化的混合单纯形搜索和粒子群优化。工程师。最佳。 36 (4), 401–418 (2004)。
-
Agrawal, A. & Tripathi, S. 基于累积二项式概率的自适应惯性权重的粒子群优化。进化。英特尔。 14 , 305–313 (2021)。
-
Nickabadi, A.、Ebadzadeh, MM 和 Safabakhsh, R。一种具有自适应惯性权重的新型粒子群优化算法。应用。软计算。 11 (4), 3658–3670 (2011)。